A differenza delle particelle cariche, i fotoni, essendo elettricamente neutri, non subiscono una continua perdita di energia durante la loro propagazione attraverso la materia. Essi possono percorrere distanze considerevoli prima di interagire con un atomo. La probabilità che un fotone interagisca con un atomo per unità di percorso è una quantità statistica che dipende sia dal mezzo attraversato sia dall’energia del fotone stesso. Quando un’interazione si verifica, il fotone può essere assorbito, scomparendo completamente, diffuso, modificando la propria direzione di propagazione o produrre coppie particella-antiparticella.

Supponendo quindi di avere un fascio di fotoni monoenergetici con intensità incidente che attraversa un materiale di densità sarà attenuato esponenzialmente dalla legge ¹ :

(1)  

dove prende il nome di coefficiente di attenuazione lineare e x la profondità a cui si valuta l’attenuazione. E’ facile intuire che il fattore rappresenta la frazione di fotoni che non collidono attraversando uno spessore x. Solitamente si e’ soliti fare riferimento alla quantità chiamata coefficiente di attenuazione di massa in quanto sperimentalmente più misurabile e che rappresenta la probabilità che un fotone interagisca con un di materia attraversata. Per cui la [1] conviene riscriverla come

(2)  

In fig.1a e fig 1.b sono riportati i coefficienti di attenuazione di massa in funzione del energia del fotone incidente per un composto, il calcestruzzo, e per un elemento, il piombo.

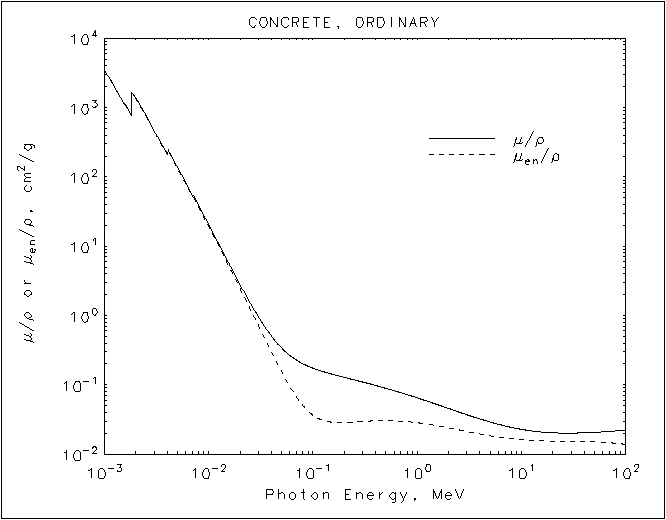
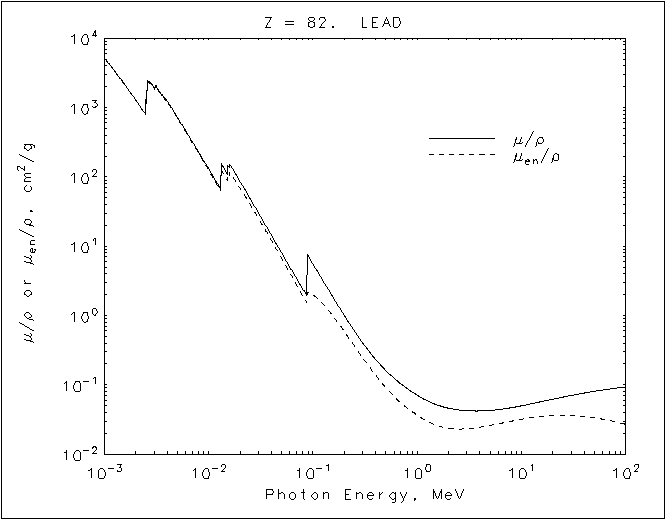
A titolo di esempio supponiamo di avere un fascio da 1 Mev e calcoliamo l’attenuazione che il fascio subisce attraversando uno strato x di 10 cm di calcestruzzo o di piombo, per il calcestruzzo sarà mentre per il piombo sarà mentre la densità dei due . Sostituendo questi valori nella 1 si ottiene :

   

   

Da cio si deduce che i 10 cm di calcestruzzo riducono del 22.4% l’intensità del fascio mentre, come ci si aspettava, altrettanti di piombo permettano a soli 0,03% del fascio di oltrepassare la barriera.

Il coefficiente di attenuazione lineare può essere espresso come somma di tre coefficienti di attenuazione lineari² :

(3)  

Che rappresentano i tre fenomeni che l’interazione dei fotoni con la materia provoca:

) effetto fotoelettrico

) diffusione da parte degli elettroni liberi (Thomson, Rayleigh e Comptorl)

) produzione di coppie elettrone-positrone

Effetto fotoelettrico

Nel 1887, Heinrich Hertz (1857-1894) scoprì che l’esposizione dell’elettrodo negativo di un circuito scintillante (un dispositivo utilizzato per generare scintille elettriche tra due elettrodi separati da una distanza d’aria) alla luce ultravioletta, facilitava il verificarsi della scintilla tra gli elettrodi a elevata tensione. Il fenomeno osservato da Hertz consisteva nel fatto che un corpo metallico carico negativamente, se esposto a raggi ultravioletti, perdeva gradualmente la sua carica. Tuttavia, illuminando allo stesso modo un corpo carico positivamente, non si riscontrava alcuna variazione di carica. Se invece il corpo non era carico, l’esposizione ai raggi ultravioletti lo portava ad acquisire una carica positiva.

Dopo la scoperta dell’elettrone nel 1897 da parte di J.J. Thomson (1856-1940), sia Thomson stesso che Philipp Lenard (1862-1941) eseguirono esperimenti per misurare la carica specifica (e/m) delle particelle emesse dai materiali sotto illuminazione. Trovarono che la carica specifica di queste particelle era identica a quella degli elettroni dei raggi catodici. Questo risultato dimostrava che i materiali, quando illuminati, emettevano effettivamente elettroni.

Tali studi furono essenziali per comprendere che il fenomeno osservato da Hertz e successivamente approfondito da Hallwachs e altri era dovuto all’emissione di elettroni dai materiali in seguito a illuminazione. Il fenomeno di emissione di elettroni dalla materia per effetto della radiazione incidente è noto come effetto fotoelettrico.

L’effetto fotoelettrico rappresenta un momento storico cruciale perché rivelò i limiti della teoria ondulatoria classica della luce, che fino alla fine del XIX secolo spiegava con successo molti fenomeni ottici. Tuttavia, le osservazioni sperimentali mostrarono che l’energia dei fotoelettroni emessi da un metallo irradiato non dipendeva dall’intensità della luce, come previsto dalla teoria classica, ma dalla frequenza della luce stessa.

Albert Einstein, nel 1905, propose una spiegazione innovativa: la luce arriva in “quanti” discreti, o fotoni, ciascuno con un’energia proporzionale alla frequenza ν del fotone, secondo la formula E=hν, dove h è la costante di Planck. Einstein ipotizzò che ogni fotoelettrone fosse emesso quando un singolo elettrone nel metallo assorbiva completamente un singolo fotone e per questo vinse il Nobel nel 1921.

Nell’assorbimento fotoelettrico, quindi, l’energia di un fotone viene spesa per rimuovere uno degli elettroni da uno strato interno di un atomo dell’elemento assorbitore. A causa della loro alta energia, i raggi gamma, a differenza della luce, possono interagire con elettroni più profondi (come quelli negli orbitali K o L degli atomi) e liberare questi elettroni interni dal materiale. Naturalmen­te questo processo può avvenire soltanto se il fotone incidente possiede un’energia più alta di quella di legame dell’elettrone in causa. In alte parole I’energia cinetica acquisita dall’elettrone reso libero è determinata dalla relazione ³ :

(4)  

dove e’ l’energia del raggio e è l’energia di ionizzazione di quel guscio al quale è stato strappato l’elettrone (i =). L’energia di rinculo acquisita dall’atomo, e più precisamente dallo ione formato, la possiamo trascurare a causa della sua piccolezza.

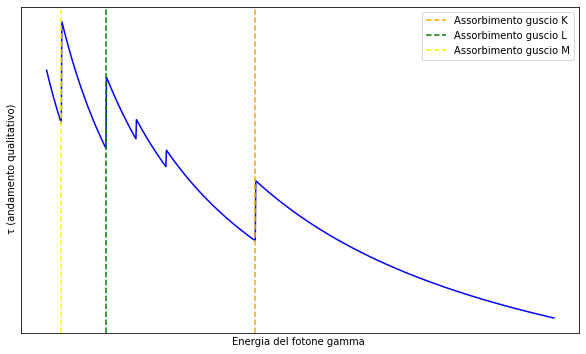
Per energie elevate, il coefficiente di assorbimento lineare dell’effetto fotoelettrico è piccolo. Al diminuire dell’energia, esso aumenta, ma quando l’energia del fotone raggiunge un valore vicino a quello del guscio K dell’atomo, diminuisce bruscamente. Questo calo è dovuto all’impossibilità per il fotone di estrarre un elettrone dal guscio K quando l’energia è insufficiente. Successivamente, al diminuire dell’energia, la sezione d’urto riprende a crescere fino a un’altra diminuzione marcata sul guscio L, che è suddiviso nei sottogusci , producendo tre denti sulla curva  come mostra la fig.2.

Oltrepassato il guscio L, il coefficiente di assorbimento lineare dell’effetto fotoelettrico cresce nuovamente al diminuire dell’energia del fotone fino al raggiungimento del guscio M, dove si verifica un’ulteriore discesa brusca, e così via. Per valori di energia del fotone inferiori a circa 0,2 MeV, diminuisce con l’energia come , mentre per energie maggiori di 0,5 MeV la diminuzione segue un andamento come

La probabilità di interazione fotoelettrica cresce con Z, ed è generalmente proporzionale a , dove n varia tra 4 e 5. Questo dipende dal fatto che, negli elementi più leggeri, gli elettroni sono legati meno fortemente rispetto agli elementi più pesanti, per cui l’effetto fotoelettrico è più rilevante nell’interazione della radiazione γ con atomi di elementi pesanti.

Al di sopra di diverse centinaia di keV l’effetto fotoelettrico da contributi minimi ed inizia ad avere importanza la diffusione per scattering.

1.https://physics.nist.gov/PhysRefData/XrayMassCoef/chap2.html

2.James E. Turner – Atoms, Radiation, and Radiation Protection (2007, Wiley-VCH) pag.87

3.Sivuchin – Fisica Nucleare – (Corso di Fisica Generale V Parte Seconda ) – Mir pag.151